When you want to print an object on a 3D printer, you will likely find that one option is a file in the STL format. In the Windows operating system, these files will generally have a “.stl” extension. If you’ve ever wondered what is in these STL files read on …
STL (STereoLithography) is a file format used to describe surfaces in CAD 3D modeling packages. The format specifies the triangles which make up the surface without any colour information.
The Wikipedia article on STL does a nice job of describing the format, but examples are generally useful.
A single triangle can be described by the file ‘tri.stl’, which contains the following:
solid trianglefacet normal 0.0 0.0 0.0 outer loop vertex 0.0 0.0 0.0 vertex 1.0 0.0 0.0 vertex 0.0 1.0 0.0 endloop endfacet endsolid triangle
If you create a file and put the contents above into it, you will be able to read the file with a suitable program. I use Paraview from Kitware. Paraview is open source software for scientific visualization, but other software able to deal with 3D geometry will also be able to read and display the file.
The red balls show the location of the three vertices and the triangle is coloured blue. The origin is in the lower left corner, the x-axis points to the right and the y-axis points up. Of course, this is only a single triangle, but it is the basic construct of much of 3D modeling and the geometry that 3D printers need to do their magic.
Now lets look at a tetrahedron with vertex coordinates:
v1: (1, 1, 1) v2: (1, −1, −1) v3: (−1, 1, −1) v4: (−1, −1, 1)
The coordinates in an STL file must all be positive numbers, so we need to translate these vertices to the first octant by adding the vector (1, 1, 1) to the coordinate vectors. This moves the centre of the tetrahedron to the point (1, 1, 1) and gives us the new vertices
v1': (2, 2, 2) v2': (2, 0, 0) v3': (0, 2, 0) v4': (0, 0, 2)
The tetrahedron is then made up of four triangles which we can specify by listing their vertices as follows:
t1: v1', v2', v3' t2: v4', v3', v2' t3: v3', v4', v1' t4: v2', v1', v4'
The order of the vertices gives the direction of the normal by the right-hand rule – the fingers of the right hand go around the direction of the vertices as listed, and the thumb points in the direction of the normal. To get the detailed normal vector you will need to use the cross product of vectors along the edges of each triangle.
The STL file for the tetrahedron will then contain the following, which can be copied into a file that you might want to name ‘tet.stl’, for example:
solid tetrahedron
facet normal 0.0 0.0 0.0
outer loop
vertex 2.0 2.0 2.0
vertex 2.0 0.0 0.0
vertex 0.0 2.0 0.0
endloop
endfacet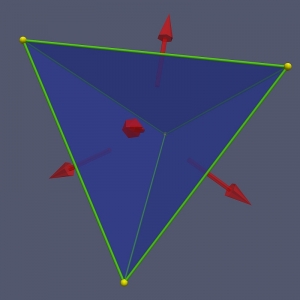 facet normal 0.0 0.0 0.0
outer loop
vertex 0.0 0.0 2.0
vertex 0.0 2.0 0.0
vertex 2.0 0.0 0.0
endloop
endfacet
facet normal 0.0 0.0 0.0
outer loop
vertex 0.0 2.0 0.0
vertex 0.0 0.0 2.0
vertex 2.0 2.0 2.0
endloop
endfacet
facet normal 0.0 0.0 0.0
outer loop
vertex 2.0 0.0 0.0
vertex 2.0 2.0 2.0
vertex 0.0 0.0 2.0
endloop
endfacet
facet normal 0.0 0.0 0.0
outer loop
vertex 0.0 0.0 2.0
vertex 0.0 2.0 0.0
vertex 2.0 0.0 0.0
endloop
endfacet
facet normal 0.0 0.0 0.0
outer loop
vertex 0.0 2.0 0.0
vertex 0.0 0.0 2.0
vertex 2.0 2.0 2.0
endloop
endfacet
facet normal 0.0 0.0 0.0
outer loop
vertex 2.0 0.0 0.0
vertex 2.0 2.0 2.0
vertex 0.0 0.0 2.0
endloop
endfacet
endsolid tetrahedron
The normal vectors in the tetrahedron STL file are often optional because the software that is reading the file can calculate the normals from the vertices given, since the order of the vertices matters. This file was read into Paraview, and the display adjusted to show yellow balls where the vertices of the tetrahedron are. The normals to the triangles are also shown.
If you want to check, or otherwise actually need them, the normal vectors for the faces above, in the same order as listed above, are
n1 = ( 0.57735, 0.57735, -0.57735] n2 = (-0.57735, -0.57735, -0.57735] n3 = (-0.57735, 0.57735, 0.57735] n4 = ( 0.57735, -0.57735, 0.57735]
Note that 1/sqrt(3) = 0.57735.
The essential idea about the STL format is that it is simply a list of triangles making up a solid. The tetrahedron is a solid because the four triangle faces completely enclose the volume. This file could be printed on a 3D printer now. Of course, most 3D models will be much more complicated than the tetrahedron, containing thousands, or possibly millions, of triangles to create a smooth surface. As models contain more triangles, they become “heavy” in the sense that your computer can have a tough time rendering the model as you interact with it. The process of modeling becomes sluggish and unpleasant. The two remedies for this are to 1) get a more powerful computer, or 2) reduce the number of triangles in your model. The second alternative can often be done without decreasing the quality of the model too much.
Should you have models with millions of triangles, the size of the file you save the model into will become a concern. There is a binary STL format which can produce much smaller files. If you are writing your own STL file exporter, you will likely want to use the binary file option.
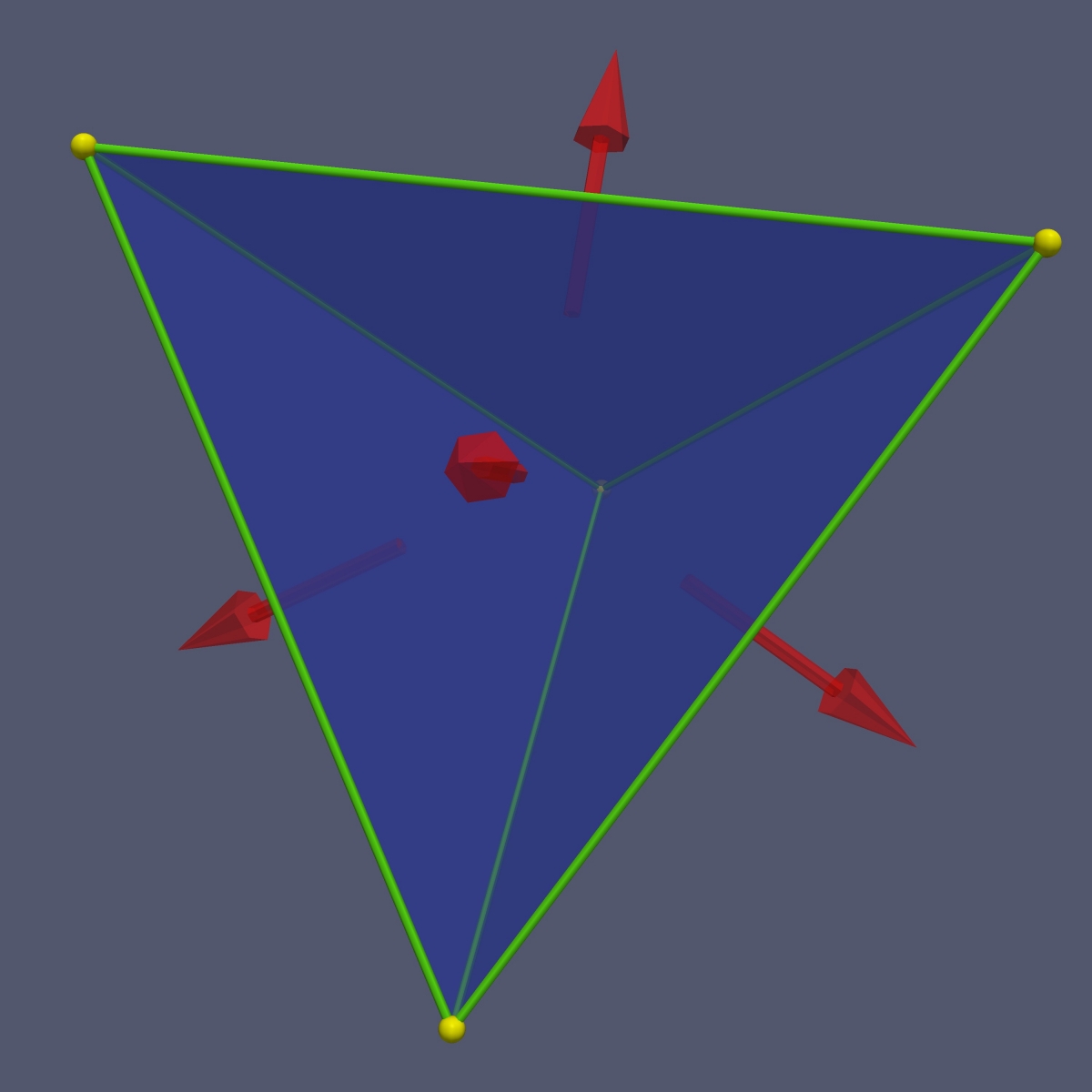
The image below is actually a 3D version of the tetrahedron, with the normal vectors. You can rotate the tetrahedron by grabbing it with a left mouse press and dragging the pointer in the direction of rotation. See the page “Interacting with WebGL On This Site”):


Leave A Comment